Por Federico Reich Weber
Director Ejecutivo de Reich Ingeniería SpA
Nuestro Director Ejecutivo y Consultor Senior tiene 47 años de experiencia y desde siempre ha sido un impulsor de nuevos planteamientos y métodos en las áreas en que lo necesite la ingeniería eléctrica.
Comenzó su carrera en 1972, en la que siendo todavía alumno en la Universidad de Chile trabajó para la Empresa Nacional de Electricidad S.A (Endesa) mientras realizaba ayudantías en su facultad. Una vez egresado, e invitado por la Universidad Católica, se desempeñó como profesor titular de la cátedra de Proyectos Eléctricos.
En las décadas siguientes trabajó en los departamentos de ingeniería eléctrica de Codelco e Indepro, para a fines de la década del 8o’ independizarse y formar junto a su actual esposa, doña Marta Baraona Valenzuela, Reich Ingeniería.
En el siguiente artículo, el ingeniero que por casi medio siglo ha estado relacionado casi por exclusividad a los proyectos eléctricos, plantea un nuevo método numérico para determinar la impedancia del retorno por tierra en lo que respecta a la componente bajo el suelo o terreno.
________________________________________________________________________________
Resumen – En cuanto a la impedancia de Carson, en principio cabe la duda de que la resistencia sea independiente de la resistividad del terreno, dado que, si la resistividad es nula, la resistencia también debería serlo, lo que implica cierta dependencia uno del otro.
Por este motivo, hemos preparado un método de cálculo numérico para la impedancia de retorno por tierra, con lo cual se determina que la resistencia es proporcional a la resistividad para valores muy bajos y pasado cierto punto, llega al valor de Carson, y desde este punto aumenta levemente pero no despreciable con la resistividad. Asimismo, la profundidad del retorno por tierra y por ende la reactancia del retorno por tierra también aumentan levemente más que lo pronosticado por Carson en función de la resistividad del terreno.
Este método numérico tiene además la ventaja de poder simular fácilmente terrenos multiestratificados, en los cuales no es aplicable la resistividad equivalente calculada por Burgsdorf-Yakobs, ya que ésta es el “equivalente serie” de las capas, usado para las mallas de puesta a tierra, mientras que para las líneas se requiere el “equivalente paralelo” de las capas.
Palabras clave: Impedancia Homopolar, Retorno por tierra, Profundidad de Carson.
1. INTRODUCCIÓN
Las líneas de transmisión de alto voltaje normalmente no producen corrientes que regresan a través del suelo, pero lo hacen en caso de un cortocircuito de una sola fase. Esta corriente debe ser calculada para ajustar adecuadamente los relés de protección. Así, la importancia de calcular la impedancia de la trayectoria de retorno de la línea de transmisión tan precisa como sea posible.
El artículo “Wave Propagation in Overhead Wires With Ground Return By JOHN R. CARSON” [1], publicado en el BELL SYSTEM TECHNICAL JOURNAL el año 1926, trata en primera instancia con este cálculo y, aunque se han publicado varios documentos adicionales sobre este asunto, todavía se utiliza para este propósito. Evidentemente, este cálculo debe tener en cuenta la resistividad del suelo en términos de ohm-m, es decir, la resistencia de un cubo de tierra de 1 m cada lado. Esta resistividad se puede medir como se explica en el estándar IEEE 81:2012 “IEEE Guide for Measuring Earth Resistivity” [2]
Sin embargo, este desarrollo tiene varios puntos que parecen no ser totalmente exactos, entre otros:
- Para la Resistencia eléctrica, establece una fórmula que depende solamente de la frecuencia y no de la resistividad eléctrica del terreno, lo que es al menos es dudoso.
- El desarrollo matemático de las fórmulas fue realizado por su colega Dr. G. A. Campbell en 1917 y no hay documentación disponible como para determinar si en el desarrollo se usaron consideraciones especiales, simplificaciones u otros aspectos que pueden alterar las fórmulas
En este artículo, vamos a establecer la formulación de un programa (para ser escrito en un programa de compilación matemática o simplemente en una hoja de cálculo) que da los principales parámetros que permiten calcular la impedancia de retorno tan preciso como un método numérico lo puede lograr.
En cierta medida, este enfoque también puede calcular la impedancia de retorno de un suelo paralelo multicapa, cuya impedancia equivalente no es la obtenida por el método Burgsdorf-Jakobs, ya que este método considera las capas principalmente en serie como en el caso de la malla de puesta a tierra en donde la corriente circula principalmente verticalmente bajo la malla.
En nuestro análisis se usarán fórmulas ampliamente conocidas en el ámbito de la electricidad y desarrolladas a partir de las ecuaciones de Maxwell.
2. PLANTEAMIENTO DEL ANÁLISIS
Para plantear el análisis se considerará un conductor aislado colocado directamente sobre la superficie el terreno, por el cual circula una corriente determinada y que retorna por el terreno con una distribución espacial que se debe determinar.
Para el caso real de un conductor suspendido en el aire se pueden usar las mismas fórmulas planteadas por Carson, tanto para la impedancia propia del circuito como para la impedancia mutua entre dos conductores suspendidos que comparten el retorno por tierra.
En la siguiente figura se muestra el esquema:
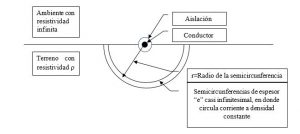
La corriente que circula por esta semicircunferencia está dada por las siguientes ecuaciones:
- La parte resistiva de la impedancia está dada simplemente por la geometría de la semicircunferencia
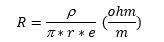
- Para el cálculo de la parte reactiva de la impedancia, de debe asumir que la profundidad media de la corriente como el radio medio geométrico de la semicircunferencia es:
![]()
Por lo tanto, la reactancia de la corriente de retorno por tierra es:
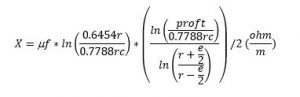
En donde:
u: 4(pi)*10-7
f: Frecuencia (ciclos por segundo)
r: Radio medio de la semicircunferencia (m)
rc: Radio del conductor en la superficie (m)
proft: Profundidad total considerada para todos los semicírculos del análisis
e: Espesor del semicírculo
Obviamente, el término 0.7788rc puede ser cambiado por el RMG del conductor si éste no es una circunferencia homogénea.
En nuestro análisis hemos considerado e = 0.005r y proft = 6383238 m (igual al radio de la tierra), sin embargo, también hemos comparado los resultados con otros valores de e para asegurar que los resultados son independientes de e, como veremos más adelante.
La primera parte de la fórmula para X, sin el factor 2, resulta del hecho que el flujo magnético entre el conductor de la superficie y el conductor equivalente al semicírculo solamente tiene componente originado por el conductor de la superficie ya que el radio medio geométrico del retorno es igual a la profundidad media, por lo que éste produce campo magnético solamente a partir de un radio que coincide con la ubicación del conductor de la superficie. La segunda parte, que corresponde al inverso de la ponderación de la semicircunferencia, se divide por 2 justamente porque toda la corriente circula por la mitad de la circunferencia completa, lo que implica la mitad de la reactancia.
La principal consideración en este análisis es que las superficies equipotenciales en el terreno son absolutamente paralelas entre ellas y perpendiculares al conductor. Esto en consideración a que la longitud de la línea es mucho mayor que la profundidad media de la corriente de retorno.
En atención a lo indicado anteriormente, se deben sumar las corrientes de todas las semicircunferencias calculadas por una diferencia de potencial determinada y la correspondiente impedancia R + jX hasta completar la profundidad total del terreno considerado, determinando finalmente la impedancia equivalente de este sistema como el cociente entre la diferencia de potencial determinada y la corriente total.
3. RESULTADOS
Primeramente, mostraremos resultados obtenidos para diversas combinaciones de f y p con un conductor con RMG = 0.01 m, con diversos valores de e, para asegurar que los resultados son razonablemente independientes de e:
| r (ohm-m) | Valores de R (ohm/km) | Valores de X (ohm/km) | |||||||
| f = (Hz) | 20 | 50 | 100 | 200 | 20 | 50 | 100 | 200 | |
| e = | 0.005r | ||||||||
| 10 | 0.02744 | 0.06431 | 0.12278 | 0.23484 | 0.26859 | 0.63302 | 1.21097 | 2.31669 | |
| 100 | 0.03276 | 0.07611 | 0.14436 | 0.27436 | 0.31213 | 0.73470 | 1.40454 | 2.68587 | |
| 1000 | 0.04007 | 0.09216 | 0.17356 | 0.32757 | 0.36466 | 0.85623 | 1.63435 | 3.12134 | |
| 10000 | 0.05040 | 0.11458 | 0.21398 | 0.40065 | 0.42965 | 1.00501 | 1.91357 | 3.64662 | |
| e = | 0.010r | ||||||||
| 10 | 0.02744 | 0.06431 | 0.12278 | 0.23483 | 0.26859 | 0.63302 | 1.21097 | 2.31669 | |
| 100 | 0.03276 | 0.07611 | 0.14436 | 0.27436 | 0.31213 | 0.73470 | 1.40454 | 2.68587 | |
| 1000 | 0.04007 | 0.09216 | 0.17355 | 0.32757 | 0.36466 | 0.85623 | 1.63435 | 3.12134 | |
| 10000 | 0.05040 | 0.11458 | 0.21397 | 0.40065 | 0.42964 | 1.00501 | 1.91356 | 3.64661 | |
| e = | 0.020r | ||||||||
| 10 | 0.02743 | 0.06431 | 0.12277 | 0.23483 | 0.26859 | 0.63302 | 1.21097 | 2.31669 | |
| 100 | 0.03276 | 0.07610 | 0.14435 | 0.27435 | 0.31213 | 0.73470 | 1.40453 | 2.68586 | |
| 1000 | 0.04006 | 0.09216 | 0.17355 | 0.32756 | 0.36466 | 0.85622 | 1.63434 | 3.12132 | |
| 10000 | 0.05040 | 0.11458 | 0.21396 | 0.40063 | 0.42964 | 1.00499 | 1.91354 | 3.64657 | |
| e = | 0.050r | ||||||||
| 10 | 0.02746 | 0.06437 | 0.12287 | 0.23501 | 0.26861 | 0.63305 | 1.21100 | 2.31666 | |
| 100 | 0.03280 | 0.07619 | 0.14451 | 0.27462 | 0.31221 | 0.73483 | 1.40474 | 2.68615 | |
| 1000 | 0.04013 | 0.09230 | 0.17379 | 0.32798 | 0.36481 | 0.85652 | 1.63482 | 3.12209 | |
| 10000 | 0.05051 | 0.11479 | 0.21434 | 0.40129 | 0.42991 | 1.00554 | 1.91445 | 3.64809 | |
A partir de estos resultados, podemos considerar que los resultados son razonablemente independientes de e y que considerando un valor de e = 0.005, los resultados son suficientemente cercanos a la realidad.
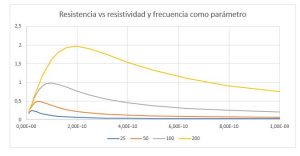
En la práctica, estos resultados ya serían suficientes para poder trabajar con ellos, pero nos interesa analizar con mayor detalle el comportamiento de estos valores con la resistividad r. Para esto analizaremos un gráfico del valor de la resistencia R en función de p para un rango amplio de p partiendo de valores muy bajos.
El siguiente gráfico muestra los valores de R para un rango de p entre 10-11 hasta 10+3 ohm-m:
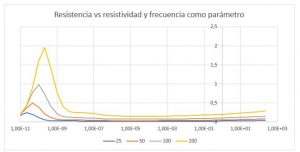
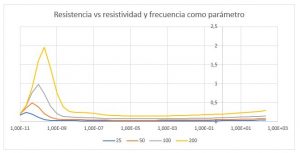
En el siguiente gráfico se muestra el rango de p entre 10-11 hasta 10-9 en escala lineal, mostrando cómo la resistencia baja a cero cuando la resistividad baja a valores muy pequeños.
Finalmente, el siguiente gráfico muestra tanto la resistencia (escala izquierda) como la reactancia (escala derecha) calculadas para 50 Hz comparadas con los valores determinados por Carson.
4. SISTEMA DE VARIAS CAPAS
Mediante este método resulta fácil analizar un terreno de varias capas aplicando los conceptos a partir de la figura siguiente, aplicable a dos capas:
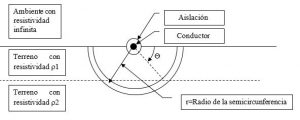
En este caso, cada segmento de la semicircunferencia se trata independientemente, para evaluarlos en paralelos, por lo tanto, las fórmulas anteriores se transforman en:
Para la capa 1:
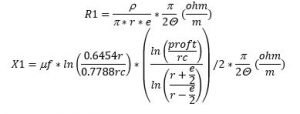
Para la capa 2:
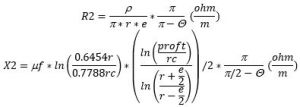
Para el paralelo de las dos capas:
![]()
Aplicando estas fórmulas, hemos calculado la impedancia y profundidad de Carson para diversas combinaciones de resistividad y espesor de la primera capa, obteniendo los siguientes resultados:
| rho1 | prof1 | rho2 | resistencia | reactancia | Profundidad de Carson |
| ohm-m | m | ohm-m | ohm/km | ohm/km | m |
| 10 | 20 | 10 | 0.06431 | 0.63302 | 237 |
| 10 | 20 | 100 | 0.09973 | 0.68618 | 553 |
| 10 | 2 | 100 | 0.07953 | 0.72990 | 1109 |
| 100 | 20 | 10 | 0.04118 | 0.67176 | 440 |
| 100 | 2 | 10 | 0.06169 | 0.63658 | 251 |
| 100 | 20 | 100 | 0.07611 | 0.73470 | 1197 |
| 100 | 20 | 1000 | 0.10497 | 0.83667 | 6069 |
| 100 | 2 | 1000 | 0.09353 | 0.85428 | 8031 |
| 1000 | 20 | 100 | 0.06570 | 0.74925 | 1509 |
| 1000 | 2 | 100 | 0.07508 | 0.73613 | 1225 |
| 1000 | 20 | 1000 | 0.09216 | 0.85623 | 8285 |
Los resultados son perfectamente consistentes y confirman la variabilidad de la resistencia.
5. CONCLUSIONES
Ante ciertas dudas que presenta el trabajo de Carson respecto a la componente resistiva de la impedancia con retorno por tierra, se plantea un método nuevo para el cálculo de esta impedancia.
En este trabajo se presenta un método numérico para determinar la impedancia del retorno por tierra en lo que respecta a la componente bajo el suelo o terreno. Estas impedancias deben ser modificadas para incluir la parte correspondiente al campo magnético en el aire, en donde interviene la altura de los conductores. Esto puede ser realizado con las fórmulas propuestas por Carson.
Se ha hecho un análisis detallado del comportamiento de la resistencia en función de la resistividad en la zona de muy baja resistividad para observar cómo se aproxima la resistencia al valor cero cuando la resistividad se aproxima a cero. En este método numérico no se puede llegar a la resistividad cero absoluto debido al cálculo de ciertas funciones que no dan resultado para este valor.
Si bien se determinó que un valor de 0.005 para el espesor relativo de cada semicircunferencia es adecuado para obtener buenos resultados para el rango usual de parámetros del terreno, hay que mencionar que la aproximación al valor cero es muy dependiente de este espesor relativo y de pequeñas sutilezas en el planteamiento de las fórmulas, lo que hace dudar del comportamiento real en este rango, pero esto no tiene más valor que puramente investigativo.
Los resultados en el rango de valores usuales del terreno, los resultados son bastante consistentes con los valores planteados por Carson, pero aumentan más que lo previsto por él cuando aumenta la resistividad del terreno.
Por otra parte, este método puede ser usado para el cálculo del retorno por tierra en terrenos estratificados, obteniéndose resultados muy consistentes. En este trabajo se propone el método para dos capas y se calcularon valores para diversas combinaciones de resistividades y espesores de la primera capa, obteniéndose valores esperables. Cabe hacer notar que en este caso no es aplicable la resistividad equivalente por el método de Burgsdorf-Jakobs que es usado para determinar la resistividad equivalente de mallas de puesta a tierra. El método planteado es fácilmente expandible a más capas usando el mismo concepto básico.
*REFERENCIAS*
[1] Wave Propagation in Overhead Wires With Ground Return By JOHN R. CARSON
[2] IEEE Guide for Measuring Earth Resistivity

